Descifrando claves de cifrado asimétrico — Implementando y vulnerando RSA

Este post documenta la resolución de un challenge de picoCTF. Se nos brinda un texto cifrado mediante un método asimétrico (RSA) y una clave pública. Para resolver el desafío, se debe desencriptar el texto cifrado.

Antes de explicar la resolución voy a explicar las bases del funcionamiento de RSA. Tras ello, dejaré el link del challenge disponible. Espero que te animes a intentarlo, en mi caso fue una tarde de mucho aprender y bastantes intentos fallidos. Al final, explico como terminé resolviendo este problema.

¿Qué es RSA?

RSA es un algoritmo de cifrado asimétrico. Esto quiere decir que requiere de dos claves, una clave pública y una privada. La clave pública esta compuesta por dos elementos:

public_key = (n,e)

La clave privada también está compuesta de dos elementos, con uno en común con la pública:

private_key = (n,d)

Para encriptar un texto, se realizan los siguientes pasos: (acompaño los pasos con un ejemplo).

Texto plano: “Hi”

Elegimos dos números primos, p y q. Para nuestro ejemplo, p=21061 y q =21163. Definimos n =p*q. Ya tenemos la primera parte de ambas claves.

Definimos un exponente “e”. Para nuestro ejemplo, e=53.

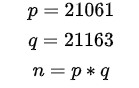
Definimos phi:

Definimos d como el inverso multiplicativo modular de phi respecto de e. Esta es una operación basada en aritmética modular, una rama de la matemática con mucho uso en criptografía. Explicarlo aquí en detalle tomaría bastante tiempo, pero en resumidas cuentas, estamos buscando un valor d tal que (e * d) % phi sea igual a 1. (% es la operación módulo) La función potencia de Python afortunadamente calcula esta operación por nosotros.

Ya disponemos de ambas claves, pública y privada. Ahora, transformamos cada carácter del texto plano en su equivalente hexadecimal. Para nuestro ejemplo, esto sería: “48 63”.

Transformamos el string resultante en un número entero. En este caso, es 115989080.

Elevamos el valor obtenido al valor e de la clave publica, y luego calculamos el modulo de dicha operación respecto de n. Es decir:

Resumen del ejemplo

C es nuestro “texto” encriptado. Para desencriptarlo requerimos de la clave privada. La operación de desencriptado es similar:

Para calcular d usamos la función pow. La misma, al usarla con el segundo parámetro en -1, funciona como inverso multiplicativo.

d= pow(phi,-1,e)

Podés probarlo con el siguiente par de scripts:

Para finalizar el ejemplo, podemos ver el código en acción:

python3 plaintext_to_rsa.py 21061 21163 53 "Hi"
Original message Hi
Hex representation of message ['48', '69']
Concatenated hex string 4869
4869
Integer representation of message 18537
18537
Encrypted message 115989080

Desencriptando:

python3 rsa_to_plaintext.py 21061 21163 53 115989080
Encrypted message: 115989080
The inverse modulus is  378400517
b'Hi'
The plaintext is Hi

El desafío

Podes ver el desafío aquí.

Nos brindan el siguiente archivo con 3 valores, el exponente, n, y el texto cifrado:

Decrypt my super sick RSA:
c:964354128913912393938480857590969826308054462950561875638492039363373779803642185
n:584586296183412107468474423529992275940096154074798537916936609523894209759157543
e: 65537

Podemos notar que n es mucho mas pequeño de lo que cabría esperar. Usualmente, es imposible descubrir p y q por factorización a partir de n. Pero en este caso, es viable intentarlo.

Alpertron nos permite realizar factoreos de números relativamente grandes. Al intentarlo, obtenemos estos resultados:

Sabemos que p y q pertenecen a estos valores. Tomando un par de los mismos, utilizamos nuestra nueva herramienta, rsa_to_plaintext.py:

#rsa_to_plain p q exponent encrypted_value
python3 rsa_to_plain.py 
p = 2434792384523484381583634042478415057961 
q = 650809615742055581459820253356987396346063
exponent = 65537
enc = 96435412891391239393848085759096982630805446295056187563849203
9363373779803642185
> The plaintext is picoCTF{sma11_N_n0_g0od_7134242}

El script nos devuelve la flag que estamos buscando. El sitio solicita en lo posible no publicar flags completas online, por lo que los últimos dígitos no son los valores reales.

Creo que lo que mas me gustó de este desafío es que ilustra cuan vulnerables pueden ser los algoritmos de cifrado si no se usan buenos valores como punto de partida. Es muy útil entender las bases de como un algoritmo funciona para poder utilizar las librerías que los implementan de manera segura.

Un saludo a todos,

Alejandro.